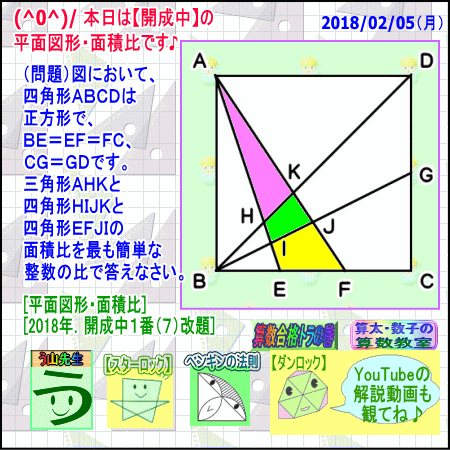
平面図形 面積比 開成中2018年 算数 数学 受験 算太数子 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ
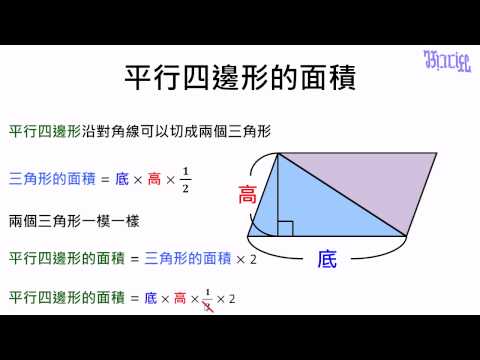
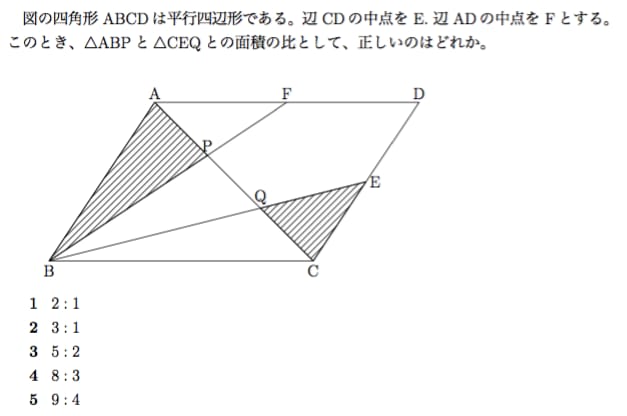
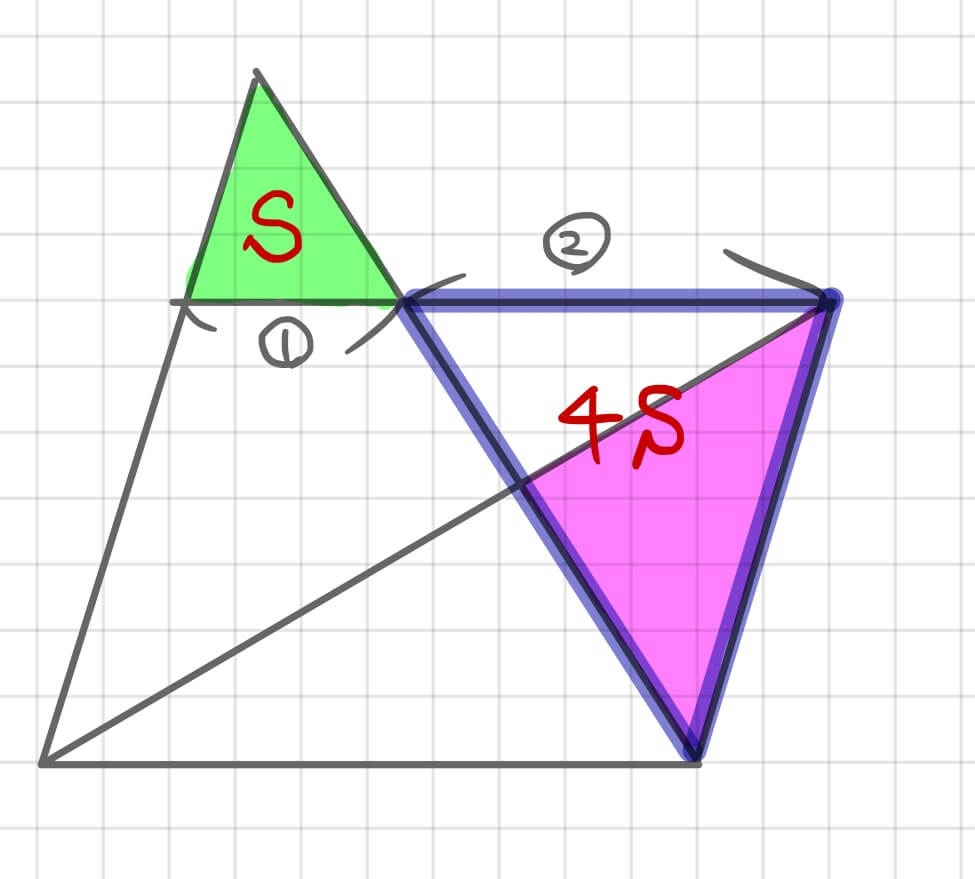
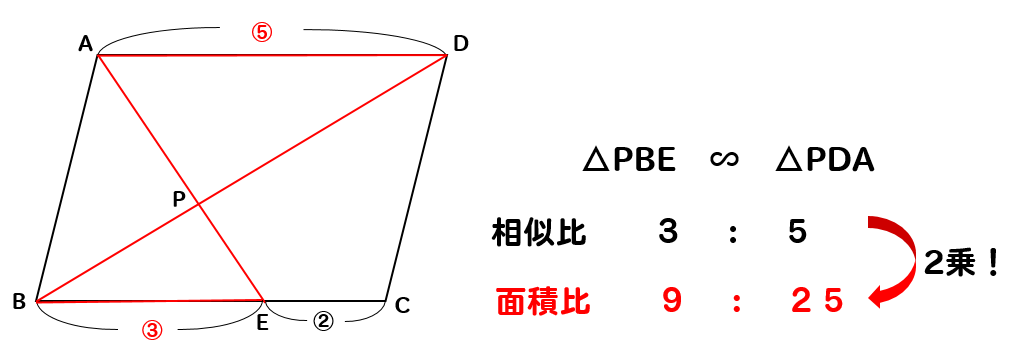
相似比は31です。 したがって、eaefも31ですし、adfcも31です。 また、四角形abcdが平行四辺形なので、辺adと辺bcの長さは同じです。辺adの長さが 3 なので、辺bcの長さも 3 です。 それをふまえた上で、下の青いチョウチョに注目してみましょう。まず、 abcの面積をsとしておきましょう。 その上で、2つのステップを踏んで解いていきます。 1つ目のステップでは、 abdと acdの面積比に注目します。 隣り合う三角形の①の型なので、底辺の比=3:5から面積比も3:5。
四角形 面積比
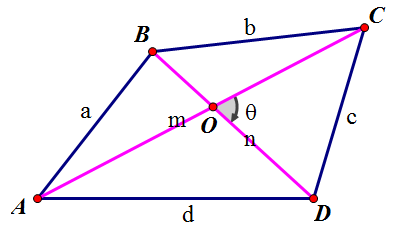
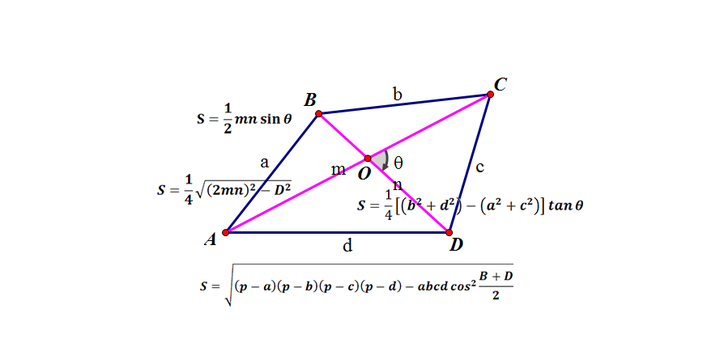
四角形 面積比-四角形の面積(4辺と対角の和から) たまたま訪れました。 この公式は,S=absin (θ1)÷2cdsin (θ2)÷2 と比較して,誤差が小さくなるのだろうか。 対角の距離を測定する手間が省けて非常に助かります。 助かりました! アンケートにご協力頂き有り難う図形と計量|正弦定理・余弦定理、面積への応用について 今回は、正弦定理や余弦定理の図形への応用を学習しましょう。 三角比を扱った総合問題です。 総合問題になると、三角形はもちろん、四角形や円とも絡めた問題も出題されます。 図形の定義
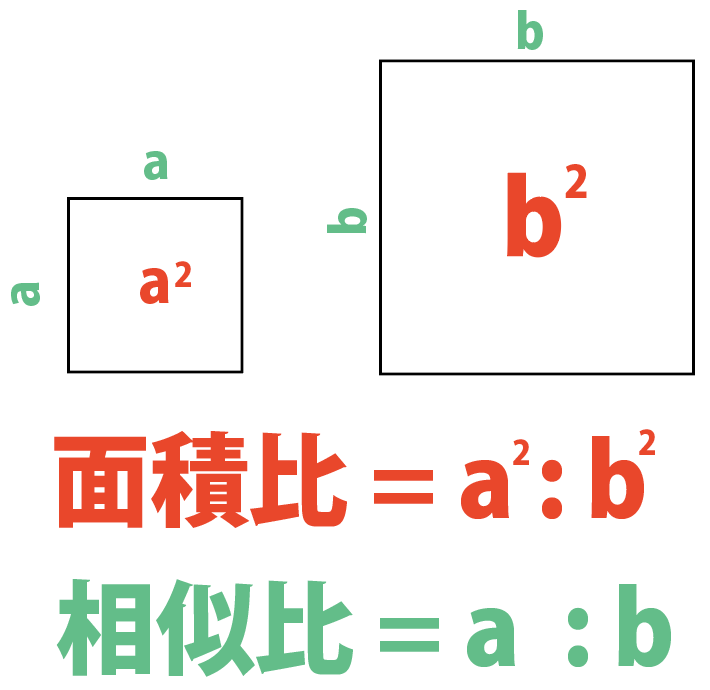
なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく
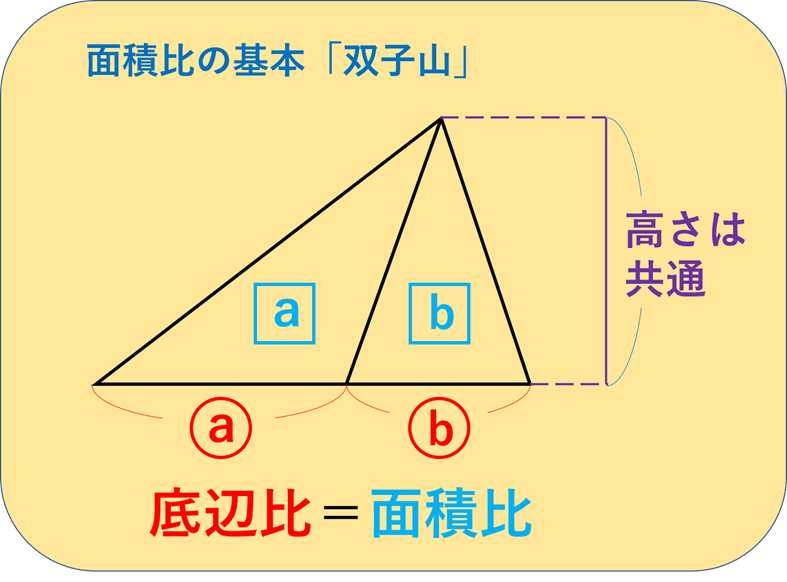
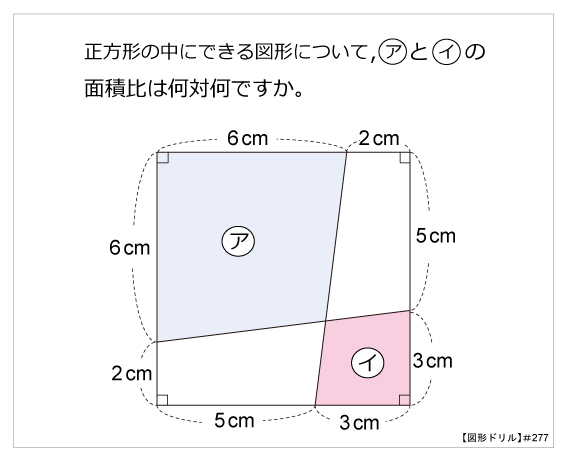
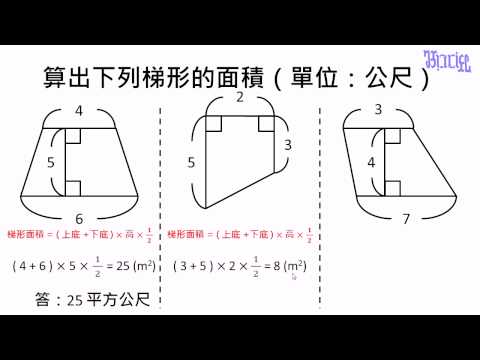
1図形の基本単位は三角形 2四角形は三角形に分割する 3補助線は1本引いただけで考えてみる 4候補の数だけ図を書いてみる 5高さの等しい三角形の面積比=底辺の比 という、5つの大切なポイントが復習できます。 「平面図形と比」の問題が苦手という第277問 2つの四角形の面積比 図形ドリル 5年生 6年生 正方形 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。
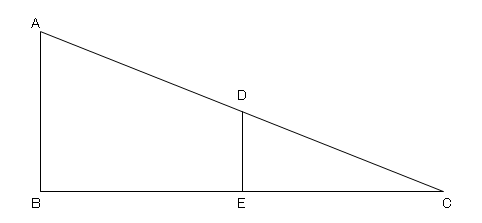
(2)四角形ghfcの面積は台形abcdの面積の何分のいくつです か? 「eggcは1:2になったから、比率をまとめると・・・」 「四角形ghfcはここ」 「どこから考えたらいいか、わからない」 「まず緑の三角形の相似比は?」 「2:2だから1:1」四角形degf:四角形ebcg 2 右の図の abcd で、辺 ad 上に点e を ae :ed=2:1 になるようにとり、bd と ec の交点を f とします。 efd=6cm2 のとき、次の図形の面積を求めなさい。 (1) cfb (2) dfc (3) 四角形abfe 相 似⑪面積比・体積比(2)a 学 年 3年角aの2等分線と辺bc の交わる点をe とするとき,三角形abeの面積と四角形aecd の面積の比を求めなさい。 ( 大妻多摩中学校 ) 『 中学入試 算数図形のまちがえるところがすっきりわかる 』(57ページ)から出題しました。
四角形 面積比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
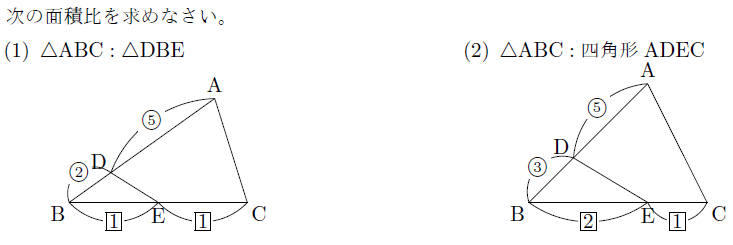 |  | |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「四角形 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
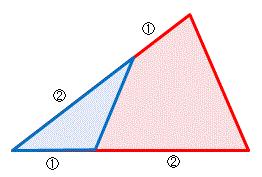
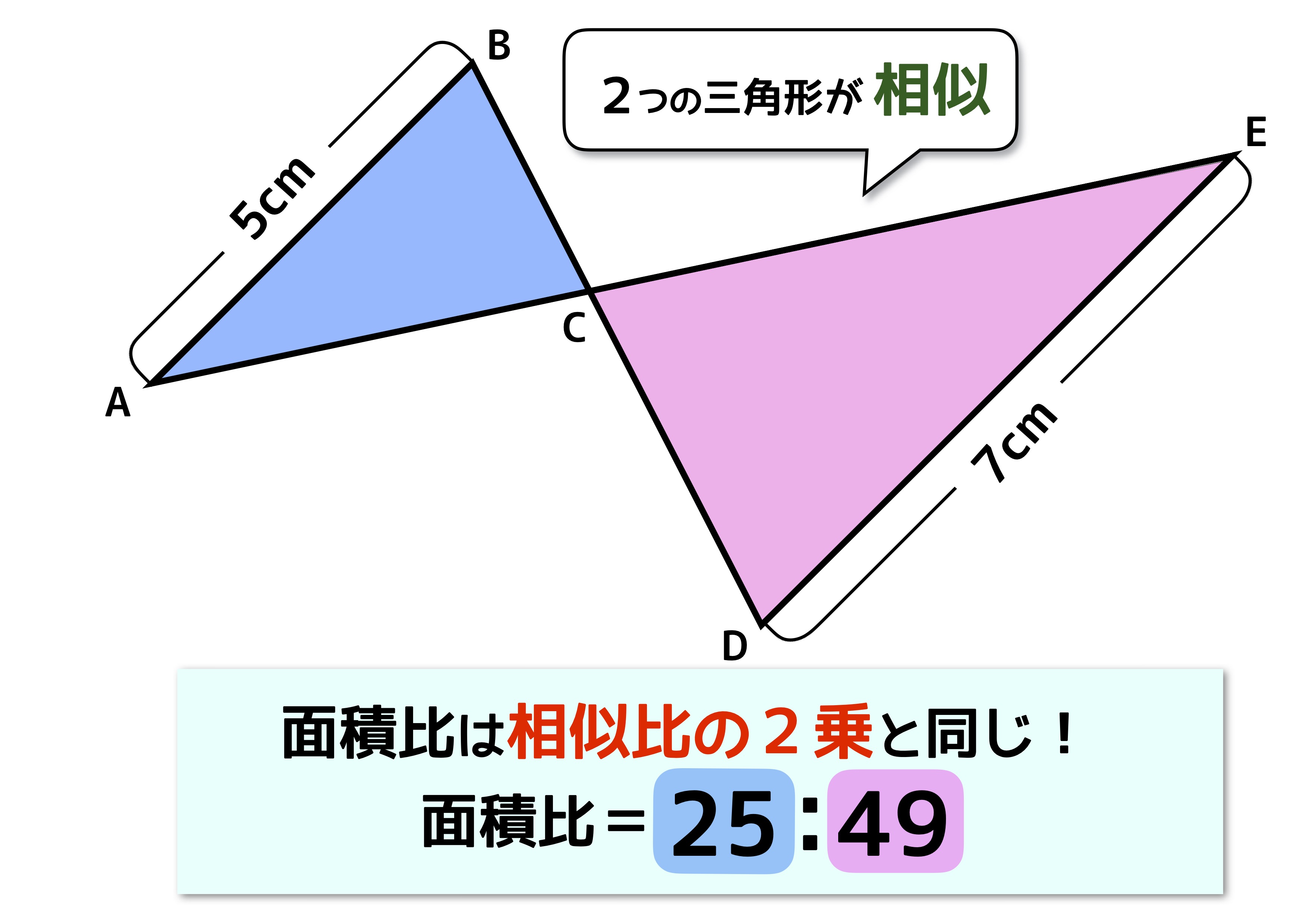
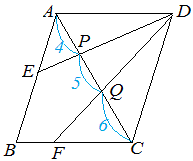
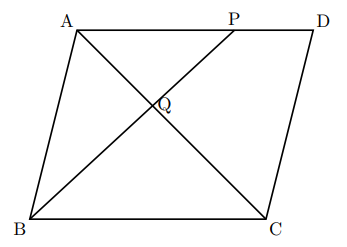
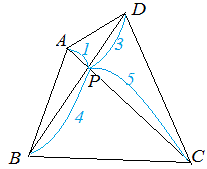
面積比に関するまとめ 今日は、まず「 相似比と面積比(体積比) 」の関係を "構成する要素の数" で明らかにしました。 その知識をもとに、三角形の面積比の公式 $3$ つ(等高・等底・等角)を導き、応用例も $2$ つ考えました。②三角形ABCと四角形PECFの面積の比を最も簡単な整数の比で求めなさい。①apを共通の底辺と考えれば、 高さの比は3:2なので、面積の比もそのまま3:2 ② d:dp=1:2なので、 黄と 緑の面積比も1:2になり、





0 件のコメント:
コメントを投稿