①対角線の長さが等しい平行四辺形は長方形である。 ②対角線が垂直に交わる平行四辺形はひし形である。①、②のそれぞれ証明がわかりません。中学生レベルで教えて貰えませんか? 1)平行四辺形ABCDにおいて、対角線を引き、 ABCと BCDとして、平行四辺形の対辺は等しいわけだからAB=AC。BCこんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明なお,四角形 abcd が平行四辺形のとき,「ðabcd」のように表すこともあります。 平行四辺形の性質③は,「対角線はたがいに他を 2 等分する」と表現してもよい。

平行四辺形 Wikipedia
平行四辺形 対角線
平行四辺形 対角線-平行四辺形の特別な形であるので、平行四辺形の性質を全て持つ。 凧形の特別な形であるので、凧形の性質を全て持つ。 正方形(スクエア、square) 4辺の長さが全て等しく、4角の大きさが全て等しい四角形。 対角線の長さは等しく、直角に交わる。力の合成が平行四辺形の対角線なら、(剛体の)天秤としてつりあっていることを示す。 上図で、点Eに力χと力yを加える。ESとERを延長する。合力は平行四辺形の対角線。 まず、どこに天秤棒と支点を作ったらいいのか。 (1)支点はAにする。




三平方の定理 平行四辺形の対角線
平行四辺形abcd対角線の交点oを通る直線をひき、ab, cdとの交点をそれぞれe、fとすると、 oe=ofとなることを証明しましょう。 aeoと cfoにおいて 平行四辺形では、対角線はそれぞれの中点で交わるのでao=co・・・① ?ので∠aoe=∠cof・・・② 正解 :対頂角は等しいブリタニカ国際大百科事典 小項目事典 平行四辺形の用語解説 2組の対辺がともに平行である四角形。次のような性質をもつ。(1) 2組の対辺の長さはそれぞれ等しい。(2) 2組の対角の大きさはそれぞれ等しい。(3) 2本の対角線はそれぞれの中点で交わる。1組の対辺が平行な四角形は台形なので 対角線bdをひくところから証明していきましょう。 個別指導塾の基本問題に挑戦! 問題 下の図のような四角形abcdがあり、点e、f、g、hはそれぞれ各辺の中点であるとする。このとき、四角形efghが平行四辺形であることを、以下のように証明した。
平行四辺形の対角線の錯視に関するメッツガー説の検討実験(浜口) すなわち,平行四辺形の左右 の斜辺が直立し,上下の辺と 直角をなすように(長方形に なるように)しようとすれば, 長対角線は圧し縮めるられる ことになるからである.逆に, 9012 2組の対角がそれぞれ等しい 121 対辺と対角が等しい証明;長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する
四角形は,1つの対角線で2つの三角形に分けることができます。 平行四辺形,ひし形,長方形,正方形は,1つの対角線で,形も 大きさも同じ2つの三角形に分けることができます。 trsA6F3tmpjtd 岩倉市日本語・ポルトガル語適応指導教室平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。平行四辺形と三角形の面積 ・平行四辺形,三角形の面積の 求め方 本単元 垂直・平行と四角 形 ・直線の垂直・平行の概念,か き方 ・平行四辺形,ひし形,台形の ・対角線の概念 5年 ・三角形,四角形の内角の和 ・縮図や拡大図の観察,性質の まとめ
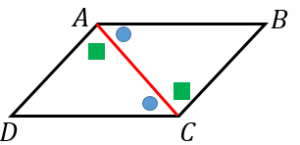



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



対角線で参観 教育考現学
次の各性質がつねに成り立つ図形に を付けなさい. (※この問題では,成り立つものはすべて ,成り立たないものはすべて としたときだけが正答となり,1つでも間違っていると正答とはなりません.各々6個のチェックボックスが完全に合っていなければ正答とはなりませんので,大変難しい平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の 面積 Sは 〔 底辺 〕×〔 高さ 〕 で求めることができる。 これは平行四辺形を面積を変えずに 長方形 に変形させることで説明できる 。〔証明〕ひし形abcdの対角線ac,bdの交点をoとする。 aboと ( )において ひし形の定義から ( )=( ) ・・・1 ひし形は平行四辺形だから 対角線はそれぞれの中点で交わるから ( )=( ) ・・・2 また
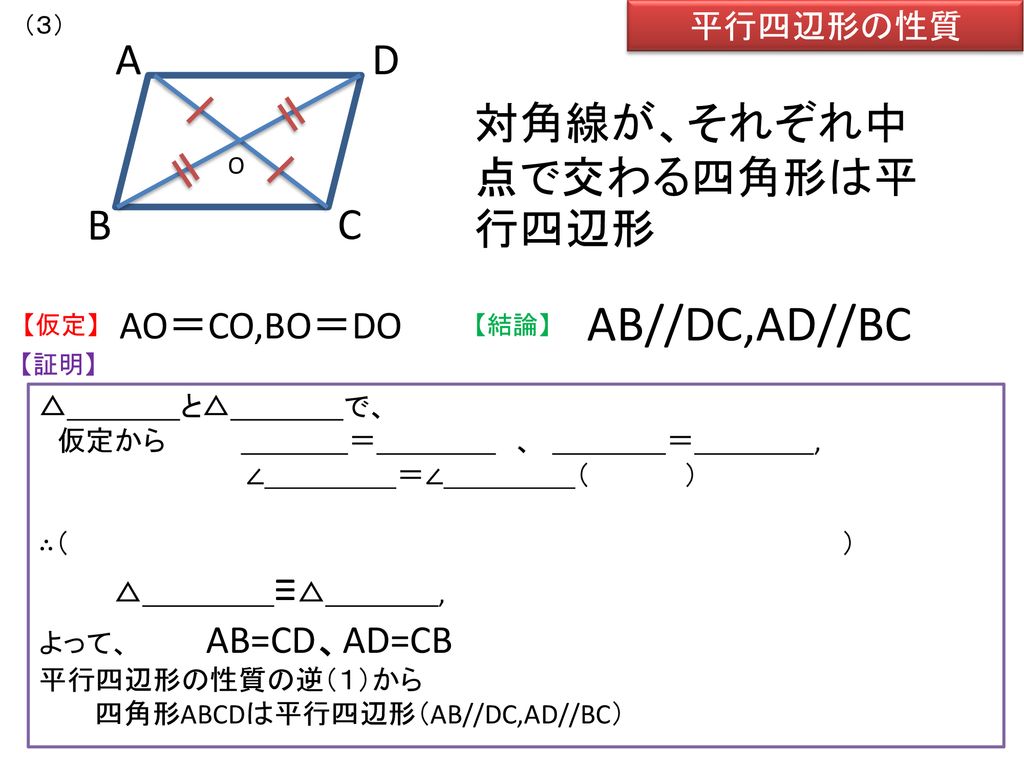



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




勉強しよう数学 余弦定理に類似した公式の多さの解決策はベクトル
平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦! それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基・平行四辺形には、下のような3つの性質があります。 1.対辺の長さが等しい 2.対角の角度が等しい 3.対角線は中点で交わる 今回、2つ目の平行四辺形の性質である、 対角の角度が等しい ことを確認していきたいと思います。四角形の、向 かい合う頂点同士をむすんだ直線のことを、対 角線といいます。 ・2 本の対角線が、それぞれのまん中の点で交わる四角形平 行四辺形、ひ し形、長 方形、正方形 ・2 本の対角線の長さが等しい四角形長 方形、正方形
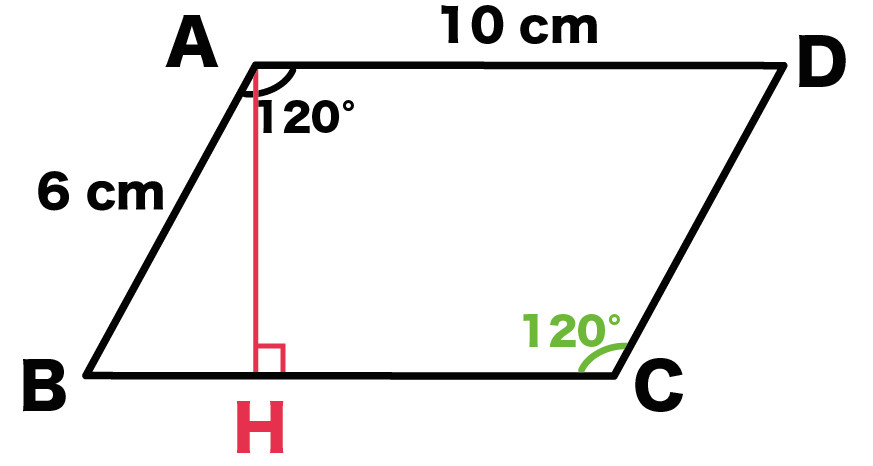



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




3 Abcd0 e Descubre Como Resolverlo En Qanda
対角線は合同です。 平行四辺形の対角線は互いに二等分します。 平行四辺形の反対側は(定義上)平行であるため、交差することはありません。 平行四辺形の面積は、その対角線の1つによって作成される三角形の面積の2倍です。※例1のような性質は「平行四辺形の2組の向かい合う辺はそれぞれ等しい」と表現されることもある. 問題 四角形 abcd について左欄の性質を証明するとき,どのような仮定からどのような結論を導けばよいか.右の欄から選びなさい. (はじめに左欄の問題を1つ選び続けて右欄の答えを選び対角線の長さが等しく、それぞれの中点で交わるとき長方形になる。 証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行四辺形abcdの性質より ab=dc 1 bc=cb(共通) 2 仮定(対角線の長さが等しい)より



Q Tbn And9gcsbpugek2jmso0mv2kzpwotsu39kazeqqzfldq4exvv7udytjh6 Usqp Cau
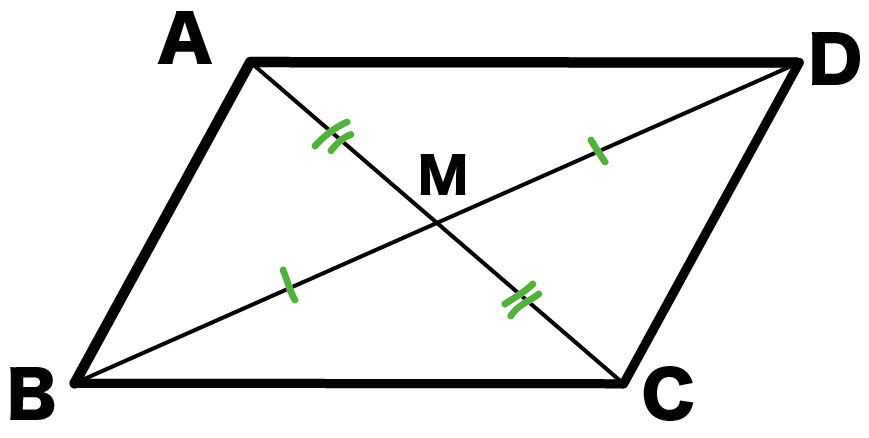



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
ひし形と正方形、平行四辺形との違い ひし形、正方形、平行四辺形の違いを下記に示します。 ひし形 ⇒ 全ての辺の長さが等しい四角形 平行四辺形 ⇒ 2組の辺の長さ等しい四角形 正方形 ⇒ 全ての辺の長さ・角度が等しい四角形 ひし形と対角線の関係4 平行四辺形の性質を利用する証明問題 問題2 図のように,平行四辺形abcdの対角線ac上にae=cfとなるように,2点e,fをとる。このとき,be=dfであることを証明しなさい。 問題の見方 平行四辺形という条件から,次の3つの性質が活用できます。14 対角線はそれぞれの中点で交わる 141 対角線が中点で交わる証明;
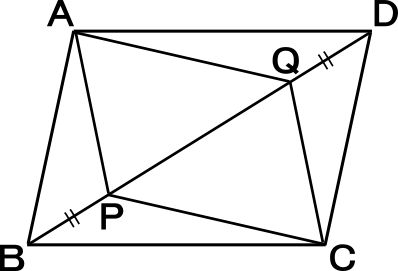



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



Http Www News Ed Jp Gimu Yumeako Gakuryoku H26 H26cyusu H26cyusua 7 Pdf
では平行四辺形の性質を定義から証明してみましょう。 平行四辺形の性質の証明 平行四辺形の定義を仮定したとき、それぞれの性質をもつことを証明しましょう。 四角形abcdにおいて対角線の交点 平行四辺形の面積を対角線の長さと角度から求める $2$ つの対角線の長さが $4$ , $6$ 、その2辺のなす角が $60°$ のとき、その平行四辺形の面積を求めよ 対角線は他の対角線の中点で交わるってことを利用して、図にするとこうなるね平行四辺形とは 向かい合う2組の辺が それぞれ平行である四辺形をいう。 対角線とは向かい合う角を結ぶ線分をいう。 (以下、定義の補足(命題1ー34)(平行四辺形・対角線)という) 平行四辺形、対角線の用語は初めてここに登場する。 対辺、対角は



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生
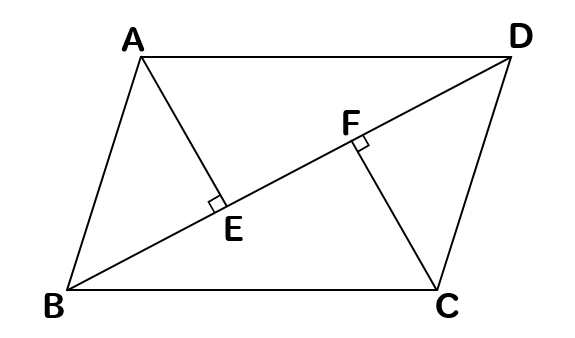



中学数学 平行四辺形の証明問題を徹底解説 数スタ
平行線の錯角は等しいので∠oab=∠ocd, ∠oba=∠odc 平行線の対辺は等しいので、ab=cd よって1組の辺とその両端の角がそれぞれ等しいので aob≡ cod 合同な図形の対応する辺は等しいのでao=co, bo=do よって平行四辺形の対角線はそれぞれの中点で交わる命題1-43(平行四辺形の補形) 対角線をはさむ平行四辺形・補形 (作図対角線をはさむ平行四辺形) すべての平行四辺形において 対角線をはさむ 二つの平行四辺形の補形は 互いに等しい。 平行四辺形は、定義の補足(命題1-34)による。∠a=∠cbe(平行線になる条件) AB//DC AD//BC <戻る> 4 対角線が、それぞれの中点で交わる。 ABOと CDOで AO=CO 1 BO=DO 2 対頂角)3 1,2,3より2辺とその間の角がそれぞれ等しいので




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
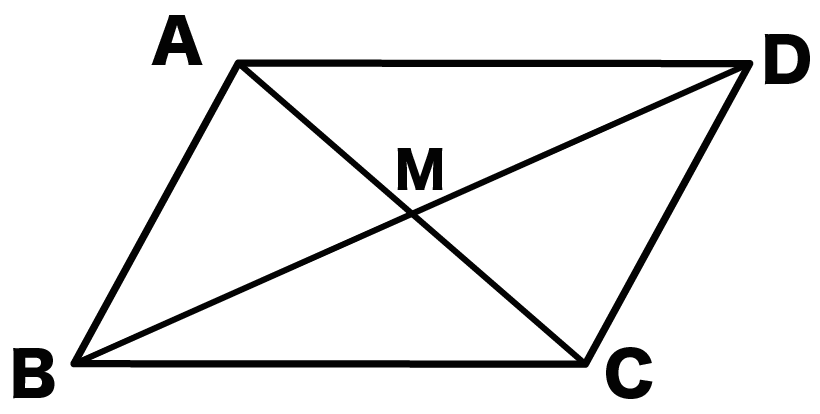



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
・平行四辺形の対角線は中点で交わります。 ・平行四辺形に対角線を引いてできた三角形は合同 なので、各辺の長さが等しいことから、 対角線は中点で交わる ことが言えます。もくじ 1 平行四辺形の定義と4つの性質 11 2組の対辺の長さが等しい;平行線の錯角、同位角 平行線の定義・・・錯角の等しい2直線は平行である。 この定義から次の性質、条件が導ける。 平行線の性質 2つの直線に1つの直線が交わるとき、 2つの直線が 平行なら錯角は等しい 。 2つの直線が 平行なら同位角は等しい 。




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題
平行四辺形とは、2組の対辺が平行な四角形 (四辺形) のことである(※1)。 問題 平行四辺形が凸四角形であることを証明してください。 この問題に驚いたと思います。中高の数学では一度も出てきませんからね。でもここは『数学事始め』なのでこういうのもときどき出てきます。4 右の図の平行四辺形で,2本の対角線の交わった点をEとします。 ⑴ 直線AEの長さは何cmですか。 〔 〕 ⑵ 対角線BDの長さは何cmですか。 〔 〕 四角形の対 たい 角 かく 線 せん 向かい合った頂 ちょう 点 てん を結 むす んだ線を対角線といいます。 四角形に




相似 平行四辺形と面積比の問題を徹底解説 数スタ




平行四辺形を使った証明 Youtube




平行四辺形 Wikipedia




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
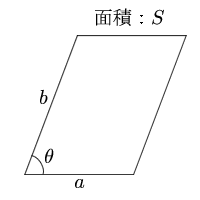



平行四辺形 2辺と間の角度 面積の計算 計算サイト
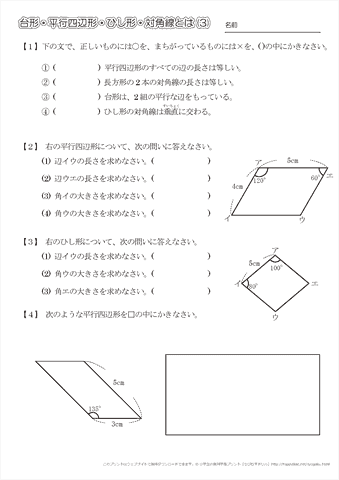



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生
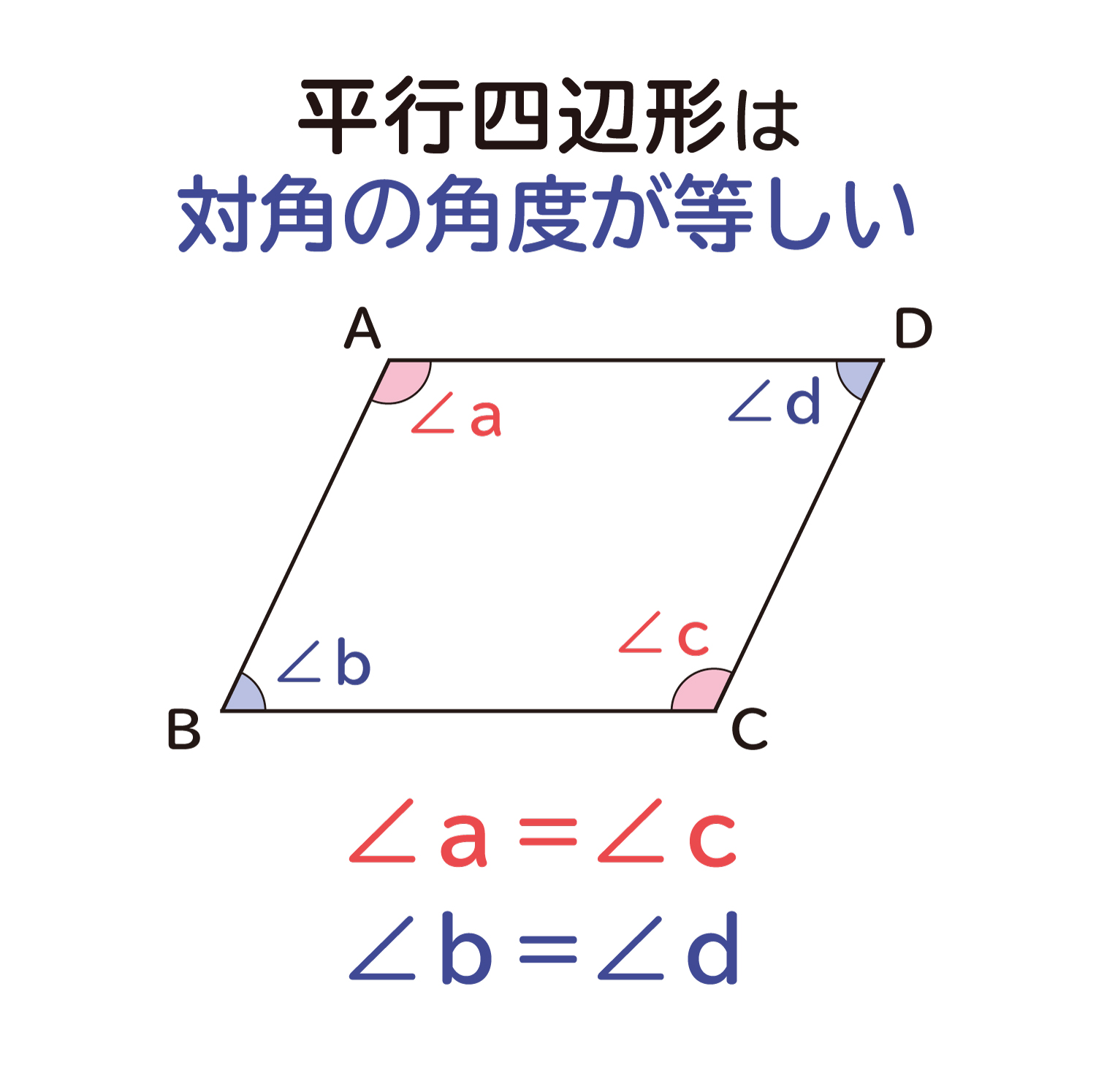



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル



平行四辺形の性質



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



第175問の解答




平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 中学校 教えて Goo




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



平行四辺形を使った証明 修正 On Vimeo




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ




平行四辺形の辺や角を求める Youtube



1




平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear




平行四辺形 Wikipedia




中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo
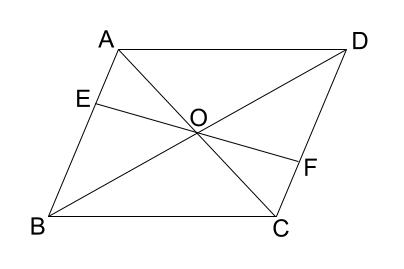



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



Math 平行四辺形 平行四辺形になることの証明 働きアリ
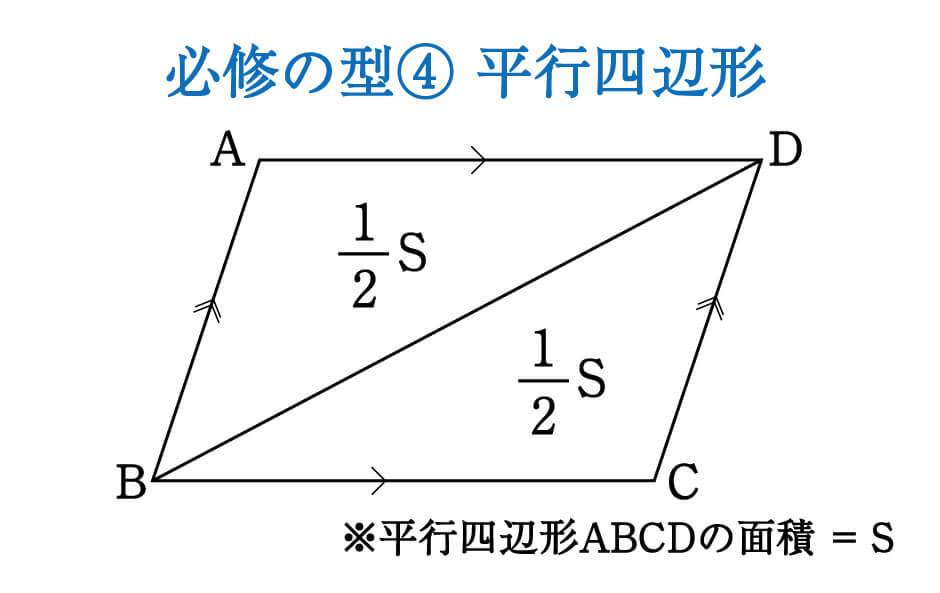



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学も英語も強くなる 意外な数学英語 Unexpected Math English Rhomboid




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
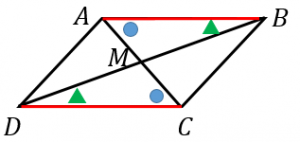



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



平行四辺形の性質の証明



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
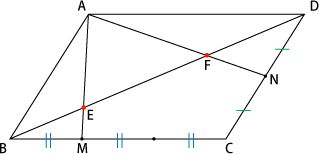



基礎学力アップシート 3年生 平行四辺形の辺の比を考えよう




平行四辺形で知っておくべきこと 苦手な数学を簡単に




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形の対角線はそれぞれの中点で交わることの証明 をしないとい 中学校 教えて Goo
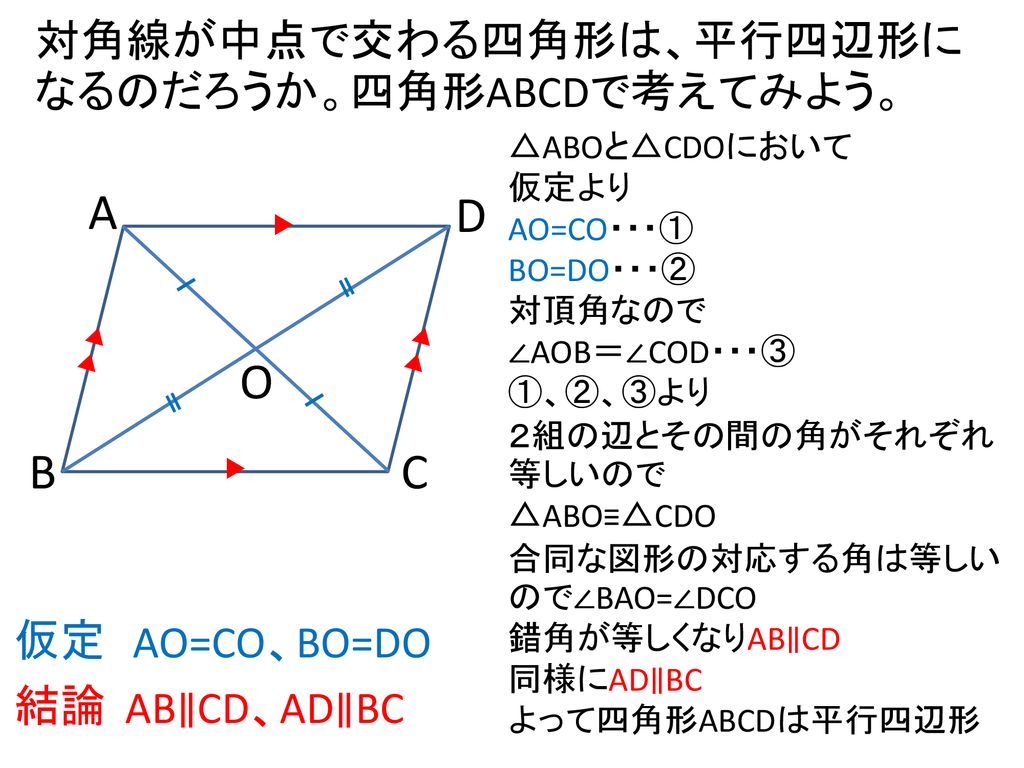



ねらい 平行四辺形の性質の逆を証明し 平行四辺形になるための条件を導くことができる Ppt Download



平行四辺形の性質の利用2




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
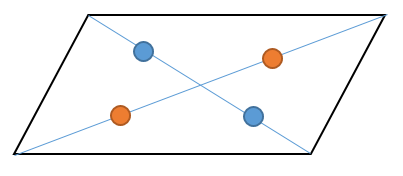



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
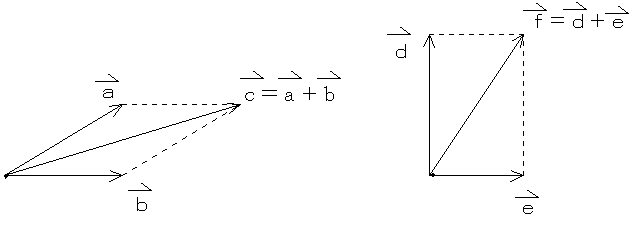



力の平行四辺形




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




z会 Asteria う 数学 点p を平行四辺形abcdの対角線acの中点にすると 平行四辺形abcdを6つの 面積が等しい 図形に分けることができます



平面図形の基礎
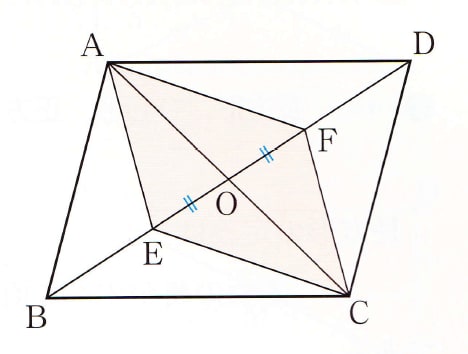



証明 は と が Takapの数学日記
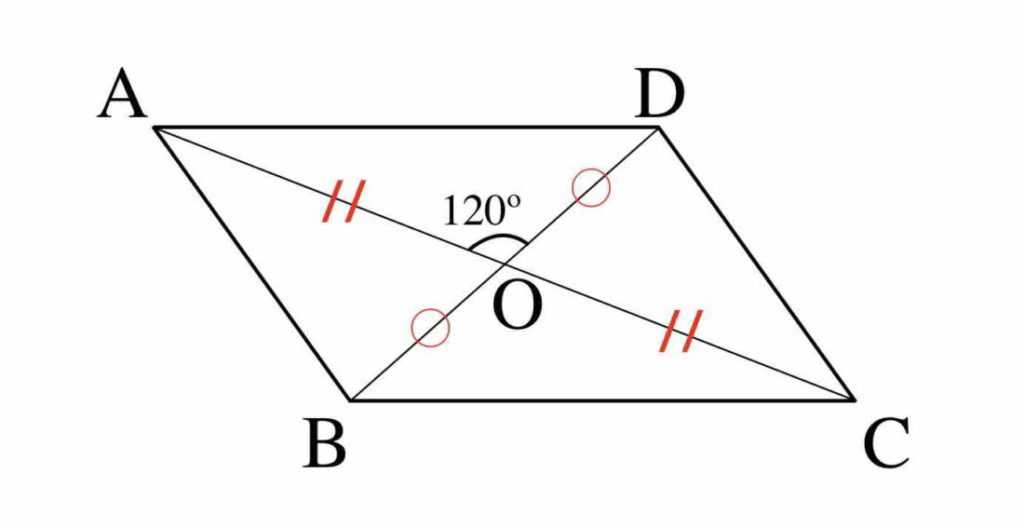



三角比を用いた面積計算をマスターしよう スタディクラブ情報局




平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear




高校数学b ベクトルの成分表示と平行四辺形 受験の月




三平方の定理 平行四辺形の対角線
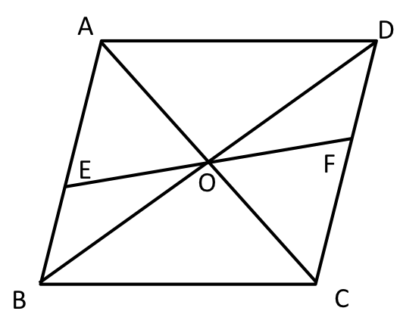



フロー 2 5 5 2 平行四辺形の性質を利用した証明




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




平行四辺形の辺や角を求める Youtube




標準 平行四辺形とベクトルの演算 なかけんの数学ノート




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



高校入試 英語 数学 学習 三角形と四角形 平行四辺形




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学



至急 数学証明平行四辺形の折り目の問題です どなたかご教示お願い致し Yahoo 知恵袋
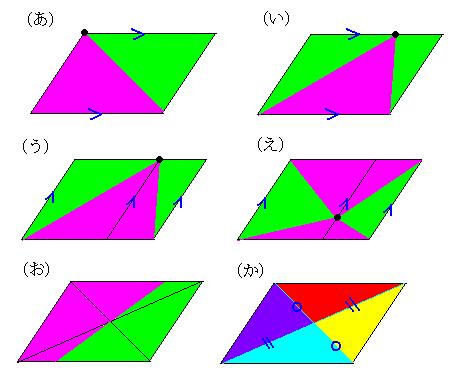



筑波大学附属駒場中学校2003年第1問 解答 解説



4年算数 垂直 平行と四角形 2 教え方



ベクトルの問題です 平行四辺形oacbにおいて 対角線の Yahoo 知恵袋




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル



大至急教えてください 下の図の平行四辺形abcdで 頂点 Yahoo 知恵袋
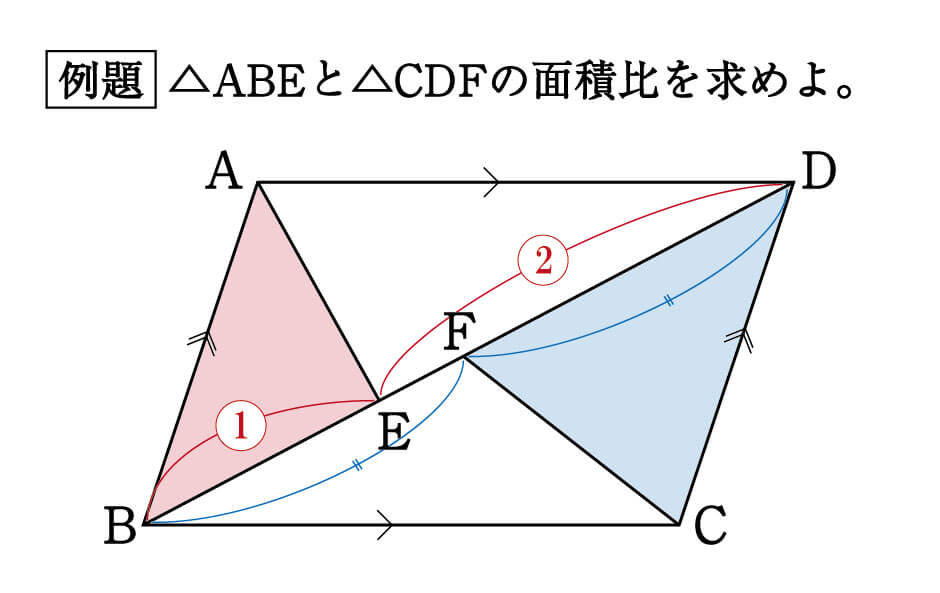



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




問6 を教えて下さい 定理 平行四辺形になるための条件 の Clear




平行四辺形の対角線の長さの求め方




平行四辺形の面積を対角線と角度から求める問題 Youtube



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd
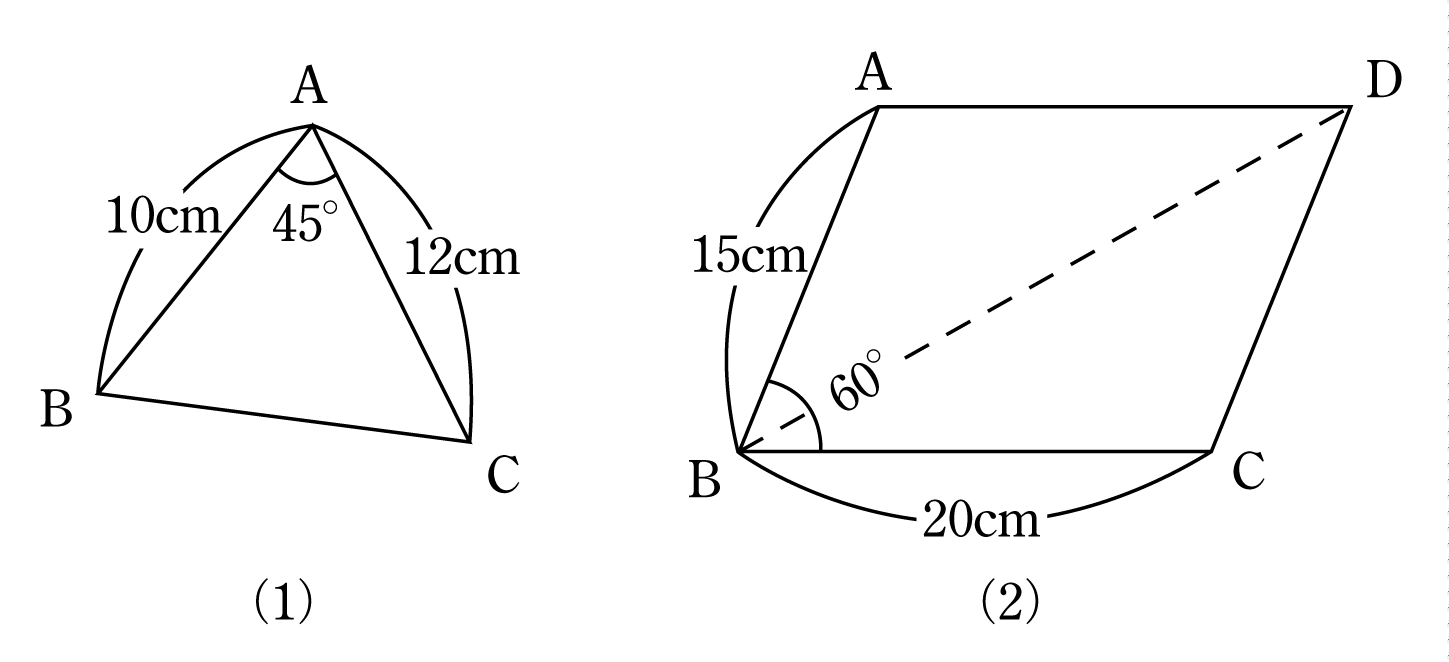



余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会
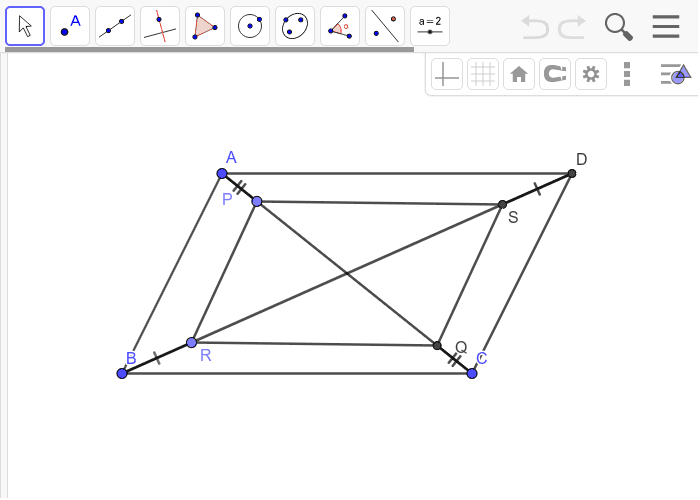



平行四辺形になるための条件 例 Geogebra



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生
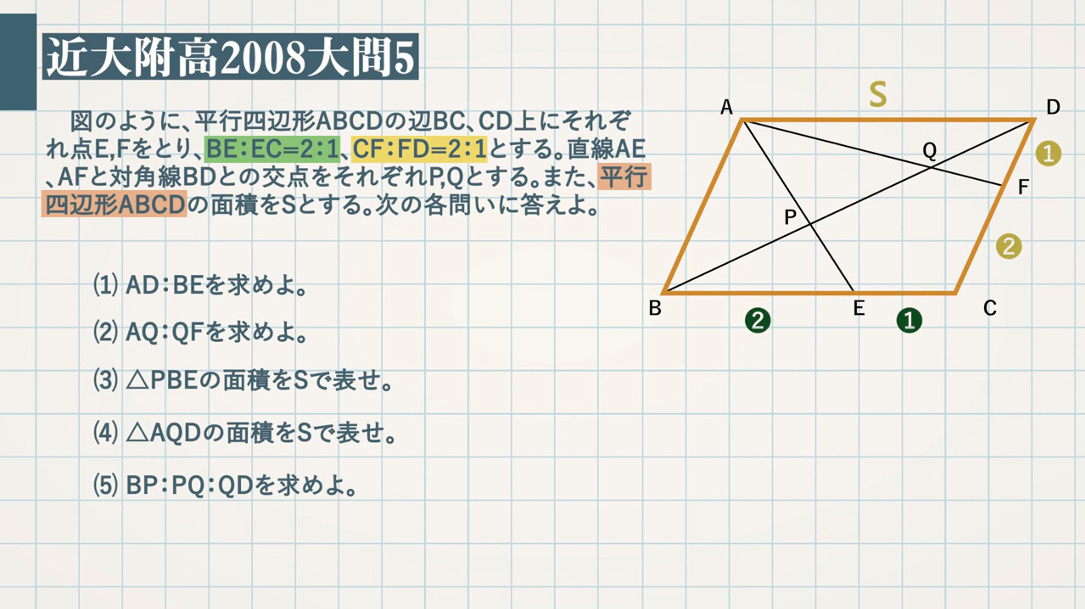



平行四辺形と比 教遊者
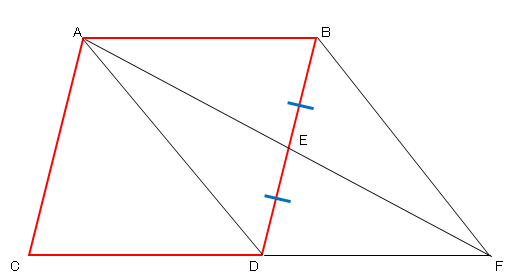



平行四辺形の証明 2 ネット塾




Cbarsquare Square Descubre Como Resolverlo En Qanda



平行四辺形について知ろう 苦手な数学を簡単に
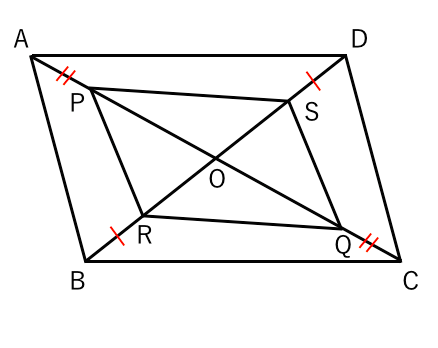



平行四辺形であることを証明する 苦手な数学を簡単に



平行四辺形の角の二等分線



今月の問題 平行四辺形



4年算数 垂直 平行と四角形 2 教え方
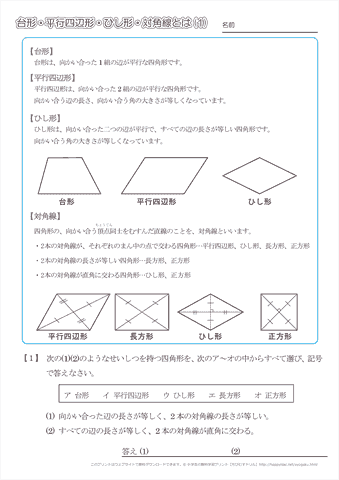



台形 平行四辺形 ひし形 対角線とは 1 台形 平行四辺形 ひし形 対角線とは 1 台形
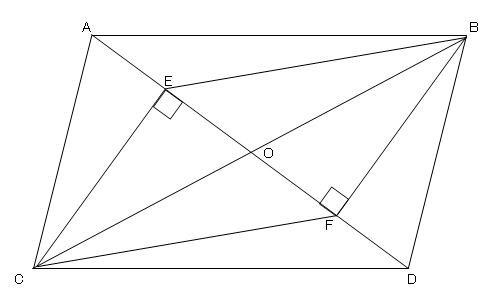



平行四辺形の証明 4 ネット塾



平行四辺形の面積の2等分




対角線と四角形 Youtube
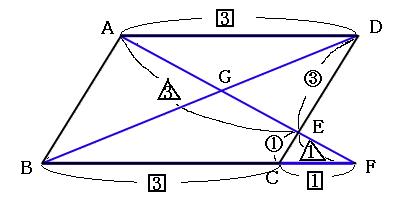



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
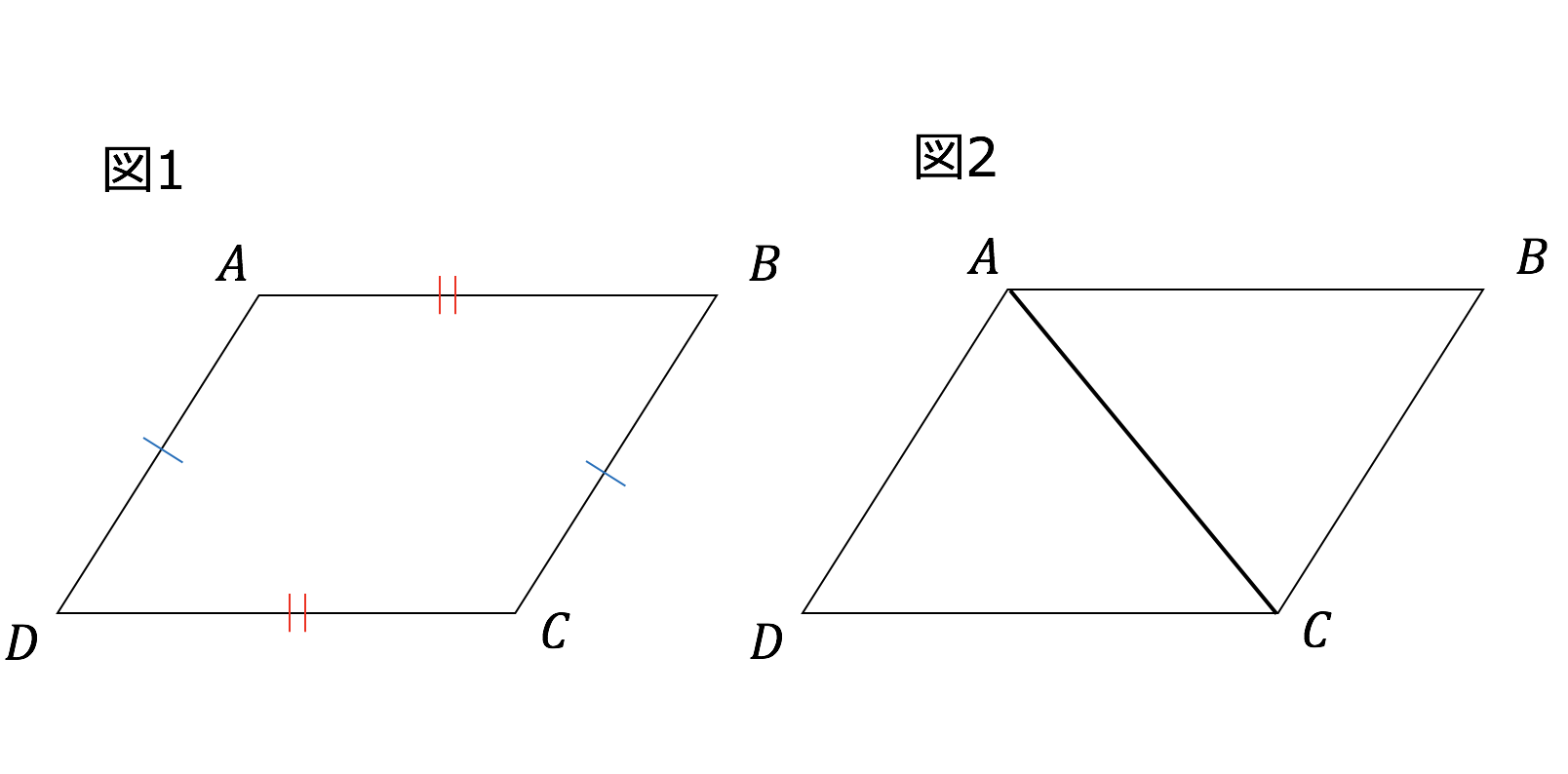



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
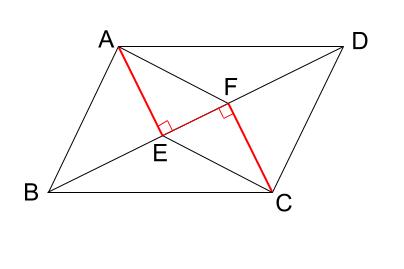



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su



1
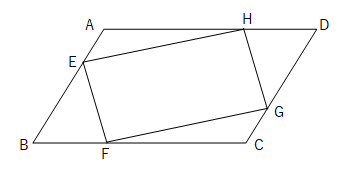



中2数学 平行四辺形の証明のポイントと練習問題 Examee
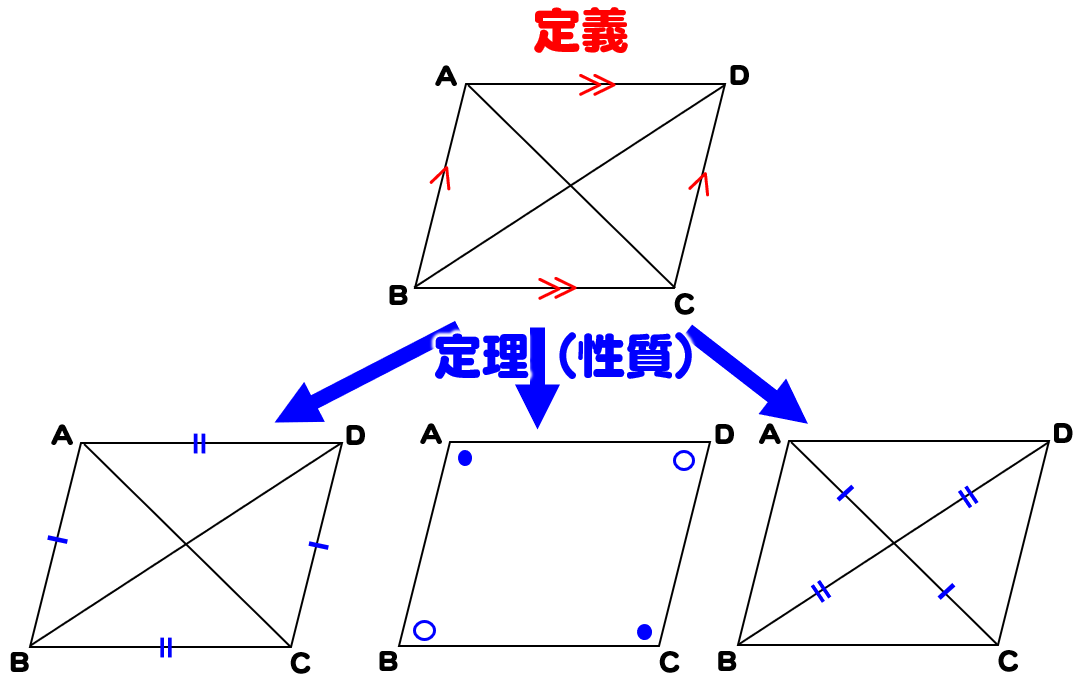



平行四辺形の定義と性質 証明問題の解き方 数学fun



1



0 件のコメント:
コメントを投稿